データ分析とは言っても、簡単なデータ分析手法はないだろうか。
データ分析を外注したいけど、何から始めればよいだろうか。
そのように思う方も少なくないのではないでしょうか。この記事では簡単でかつビジネスシーンでよく使われるデータ分析手法について紹介していきます。

1. 集計分析
集計分析は、ビジネス上で最も基本的かつ重要なデータ分析手法の一つです。ビジネスにおける様々なデータを収集し、要約し、洞察を得るために使用されます。
1.1. 集計分析の概要
集計分析は、データの要約とパターンの発見に焦点を当てます。多くの場合、数値データやカテゴリーデータを合計、平均、最大値、最小値などの統計的指標に基づいて集計し、その結果をグラフや表などで可視化します。
1.2. ビジネスでの集計分析の利用例
データの集計は、ビジネスにおけるさまざまなシナリオで活用されます。
- 売上データの集計: 売上データを日次、週次、月次で集計することで、売上の傾向や季節性を把握し、マーケティング戦略や在庫管理の最適化に活用することができます。
- 顧客データの集計: 顧客の属性や行動データを集計し、顧客セグメントを作成することで、ターゲット市場やニーズの特定、マーケティング施策のパーソナライズに活用することができます。
- 生産データの集計: 生産プロセスのデータを集計し、生産性や効率性を評価することで、生産計画の最適化や生産プロセスの改善に活用することができます。
データの集計を通じて、ビジネスにおける課題や機会をより深く理解し、効果的な意思決定を行うことができます。
1.3. 集計分析の手法
集計分析には様々な手法がありますが、代表的なものには次のようなものがあります。
- 総計の算出: データの合計値を計算して全体像を把握する。
- 平均値の算出: データの平均値を算出し、データの中心傾向を把握する。
- 最大値・最小値の特定: データの最大値や最小値を特定し、業績のピークや底を把握する。
- 頻度分析: カテゴリーデータの出現頻度を分析し、データの分布を把握する。
1.4. 集計分析の注意点
集計分析を行う際には、以下のような注意点があります。
- データの品質: 入力データの品質が集計結果に大きな影響を与えるため、データの正確性を確保することが重要です。
- 外れ値の除外: 極端な値や異常値が集計結果に歪みをもたらす可能性があるため、必要に応じて外れ値の除外を行うことが望ましいです。
- コンテキストの理解: 集計結果を解釈する際には、その背景やコンテキストを理解することが重要です。
2. 相関分析
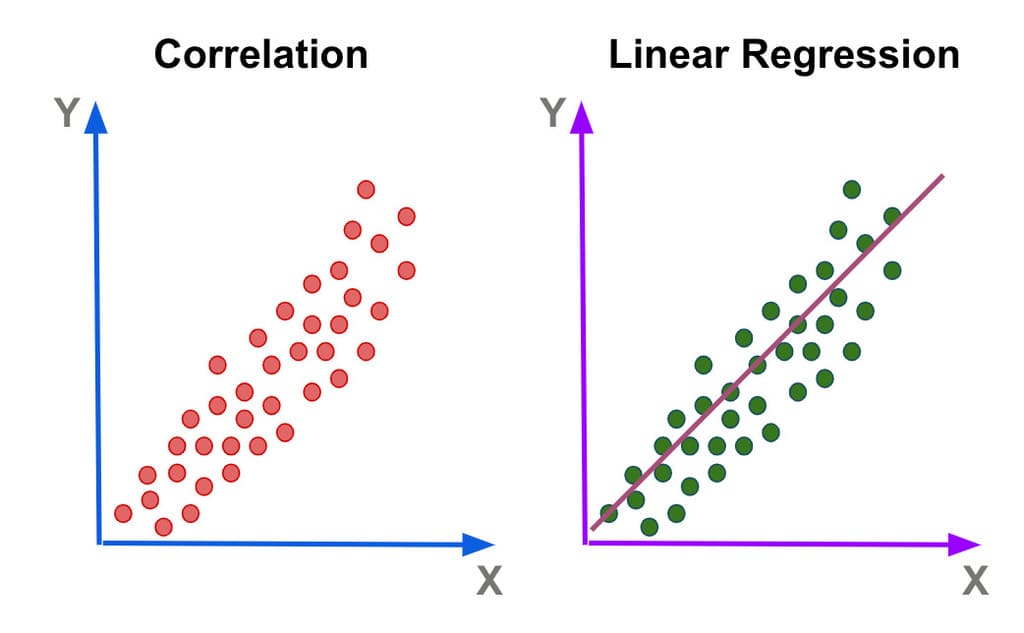
相関分析は、2つ以上の変数間の関係性を調査するためのデータ分析手法です。ビジネス上のさまざまな要因や指標の関係性を理解し、影響を評価する際に利用されます。
2.1. 相関分析の概要
相関分析は、変数間の関係性の強さや方向性を測定することを目的としています。一般的に、相関係数と呼ばれる統計量を計算して、変数間の関係性の強さを評価します。相関係数は、-1から+1までの値を取り、-1に近いほど強い負の相関、+1に近いほど強い正の相関があることを示します。
2.2. ビジネスでの相関分析の利用例
ビジネス上では、相関分析がさまざまな場面で活用されます。例えば、マーケティング活動の費用と売上の関係性を調査し、効果的な広告戦略を立案することができます。また、製品の特徴と顧客満足度の間の関係性を分析して、製品改善の方向性を見出すことも可能です。
相関分析は、ビジネスにおいてさまざまな場面で活用されます。
- マーケティング戦略の評価: 広告費と売上の相関を調査することで、どの広告施策が売上に寄与しているかを評価し、効果的なマーケティング戦略を立案することができます。
- 製品特性の評価: 製品の特徴と顧客満足度の相関を分析し、顧客が製品のどの特性に価値を見出しているかを把握することができます。
- 労働生産性の向上: 労働生産性と従業員満足度の相関を調査し、従業員の満足度向上が生産性の向上にどのような影響を与えるかを評価することができます。
2.3. 相関分析の手法
相関分析には、主にピアソン相関係数やスピアマンの順位相関係数などの統計手法が使用されます。これらの手法は、変数の種類やデータの分布に応じて適切な方法を選択することが重要です。
2.4. 相関分析の注意点
相関分析を行う際には、以下のような注意点があります。
- 相関は因果関係を示さない: 相関関係がある場合でも、因果関係があるとは限りません。他の要因や外部の影響も考慮する必要があります。
- 外れ値の影響: 外れ値がある場合、相関係数に影響を与える可能性があるため、適切な処理が必要です。
- サンプルサイズの重要性: 相関分析の信頼性はサンプルサイズにも依存するため、適切なサンプルサイズを確保することが重要です。
3. 回帰分析
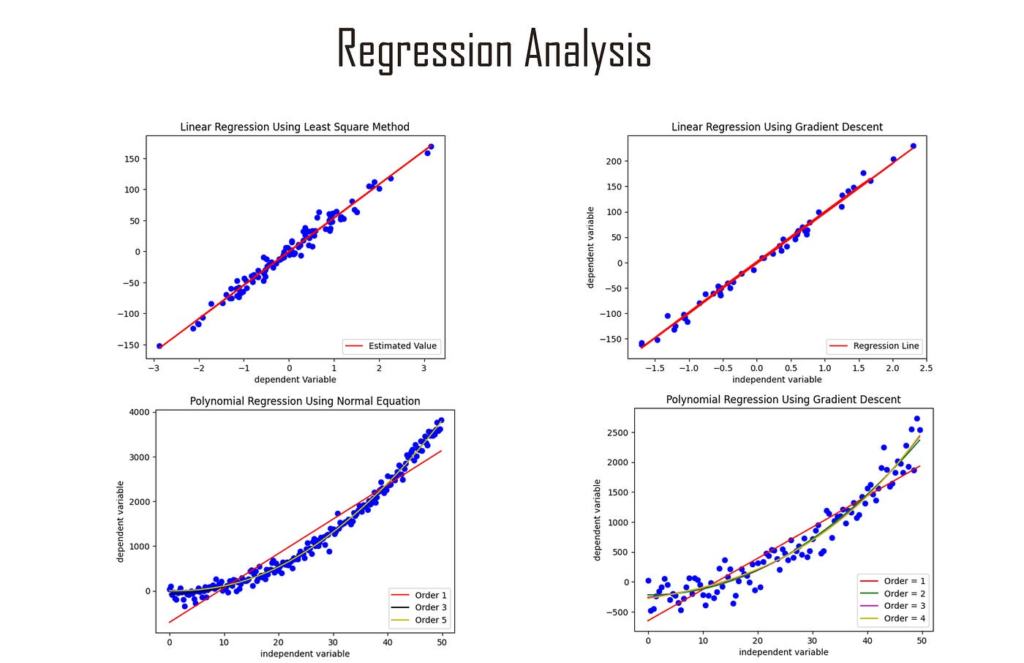
回帰分析は、1つ以上の説明変数が目的変数に与える影響を調査するための統計手法です。ビジネスにおいては、特定の要因が特定の結果にどの程度影響を与えるかを理解し、予測するために使用されます。
3.1. 回帰分析の概要
回帰分析は、説明変数と目的変数の間の関係性をモデル化することによって行われます。一般的に、最も一般的な形式である単回帰分析では、1つの説明変数が1つの目的変数に与える影響を調査します。複数の説明変数を含む重回帰分析では、複数の要因が目的変数に与える影響を同時に評価します。
3.2. ビジネスでの回帰分析の利用例
ビジネスにおいて、回帰分析はさまざまな場面で活用されます。例えば、広告費の増加が売上に与える効果を分析することで、効果的なマーケティング戦略を策定することができます。また、製品の価格が売上や利益に与える影響を評価し、価格戦略を最適化することも可能です。
回帰分析は、ビジネスにおいてさまざまな目的で活用されます。
- 売上予測: 過去の売上データをもとに、マーケティング費用や季節性などの要因との関係を分析し、将来の売上を予測します。これにより、需要予測や生産計画の立案に役立ちます。
- 価格設定: 製品の価格と売上の関係を調査し、価格戦略の最適化や競合分析に活用します。また、価格と顧客満足度との関係を分析し、価格設定に影響を与える要因を把握します。
- 顧客行動の分析: 顧客の属性や行動パターンと購買行動の関係を分析し、顧客セグメントの特定やターゲティング戦略の改善に活用します。
3.3. 回帰分析の手法
回帰分析には、様々な手法がありますが、最も一般的な手法は最小二乗法です。この手法では、誤差の平方和が最小となるようなパラメータを推定します。また、回帰モデルの選択や評価には、適切なモデル選択基準や評価指標を使用することが重要です。
3.4. 回帰分析の注意点
回帰分析を行う際には、以下のような注意点があります。
- 共変量の選択: 回帰モデルに含める説明変数の選択は重要であり、ビジネスのコンテキストや理論的根拠に基づいて適切な変数を選択する必要があります。
- 多重共線性: 説明変数間に相関が強い場合、多重共線性が発生し、推定されたパラメータの信頼性が低下する可能性があります。この問題を避けるために、説明変数の選択やデータの前処理が重要です。
- 過剰適合のリスク: 説明変数を過剰に増やすと、過剰適合のリスクが高まります。適切なモデルの複雑さを選択することが重要です。
4. クラスタリング
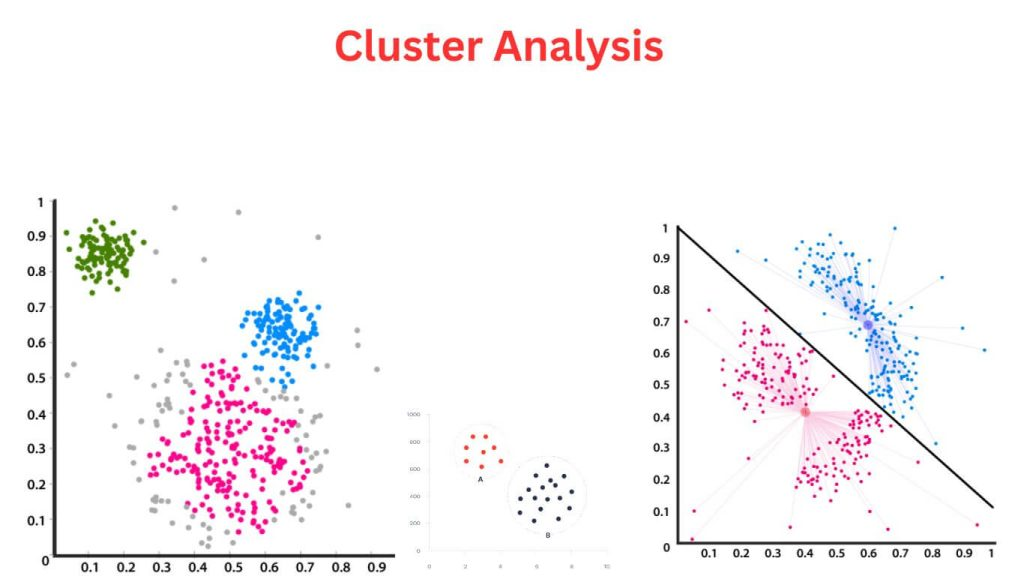
クラスタリングは、データを自然なグループやクラスタに分割する手法であり、データの構造を理解するために広く使用されています。ビジネスにおいては、顧客セグメンテーションや製品の分類などの課題に応用されます。
4.1. クラスタリングの概要
クラスタリングは、類似した特性を持つデータポイントを同じグループに割り当てることで行われます。各クラスタは異なる特性を持ち、同じクラスタ内のデータポイントはできるだけ似ているように、異なるクラスタのデータポイントとは異なるようになります。
4.2. ビジネスでのクラスタリングの利用例
ビジネスにおいて、クラスタリングはさまざまな目的で活用されます。例えば、顧客データを基に顧客セグメントを作成し、それぞれのセグメントに合ったマーケティング戦略を展開することができます。また、製品の特徴や需要に基づいて製品を分類し、製品ラインの最適化を行うことも可能です。
クラスタリングは、ビジネスにおいてさまざまな分野で活用されます。
- 顧客セグメンテーション: 顧客データをクラスタリングすることで、顧客の異なるグループを特定し、それぞれのグループの特性やニーズを理解することができます。これにより、ターゲット市場をより細かく定義し、ターゲティングされたマーケティング施策を展開することができます。
- 商品カテゴリ分類: 商品の特性や顧客の購買行動をもとに、商品を類似性に基づいてグループに分類することができます。これにより、類似した商品を同じカテゴリにまとめ、効果的な商品マネジメントを行うことができます。
- リスク管理: 金融業界では、顧客の信用リスクや投資リスクをクラスタリングすることで、リスクの異なるグループを特定し、リスク管理の効率化やリスク軽減策の策定に活用されます。
4.3. クラスタリングの手法
クラスタリングには、様々な手法がありますが、代表的な手法には次のようなものがあります。
- K-meansクラスタリング: データをK個のクラスタに分割し、各クラスタの中心を求める手法。
- 階層的クラスタリング: データを階層的にグループ化し、類似したクラスタを結合する手法。
- DBSCAN: 密度に基づいてクラスタを特定する手法。
4.4. クラスタリングの注意点
クラスタリングを行う際には、以下のような注意点があります。
- 適切なクラスタ数の選択: クラスタ数の選択は重要であり、適切なクラスタ数を選択することが必要です。
- 初期中心の選択: K-meansクラスタリングのようなアルゴリズムでは、初期中心の選択が結果に影響を与えるため、適切な初期化方法を選択する必要があります。
- 特徴量の選択: クラスタリングの結果は、使用する特徴量に大きく依存するため、適切な特徴量の選択が重要です。
5. 時系列分析
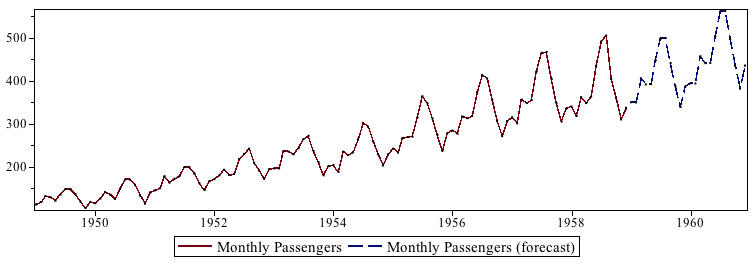
時系列分析は、時間の経過に伴うデータの変化を分析する手法であり、ビジネスにおいては将来のトレンドやパターンを予測するために広く使用されます。
5.1. 時系列分析の概要
時系列分析は、時間の経過に伴うデータの変化を理解し、モデル化することに焦点を当てます。一般的に、時間の経過に応じて観測されたデータポイントから、トレンド、季節性、サイクルなどのパターンを抽出し、将来の値を予測するためのモデルを構築します。
5.2. ビジネスでの時系列分析の利用例
時系列分析は、ビジネスにおいてさまざまな目的で活用されます。例えば、過去の売上データを分析し、将来の売上予測を行うことで、需要の変動に対応した在庫管理や生産計画を立てることができます。また、マーケティングキャンペーンの効果を追跡し、効果的な施策を見つけるためにも使用されます。
時系列データの分析は、ビジネスにおいて様々な分野で活用されます。
- 需要予測: 過去の売上データや顧客の購買履歴を分析し、将来の需要を予測することで、生産計画や在庫管理の最適化を行います。
- 財務分析: 企業の財務データを分析し、将来の収益やキャッシュフローの予測を行うことで、投資や資金調達の意思決定を支援します。
- マーケティング効果の評価: マーケティングキャンペーンの実施後、時系列データの変化を分析し、キャンペーンの効果を評価します。
5.3. 時系列分析の手法
時系列分析には、様々な手法がありますが、代表的な手法には次のようなものがあります。
- 移動平均法: 時系列データの平滑化やトレンドの推定に使用されます。
- 指数平滑法: 時系列データの平滑化や予測に使用され、新しいデータに対する重み付けを行います。
- ARIMAモデル: 自己相関と移動平均の組み合わせで時系列データをモデル化し、予測を行います。
5.4. 時系列分析の注意点
時系列分析を行う際には、以下のような注意点があります。
- データのトレンドと季節性の考慮: 時系列データにはトレンドや季節性が含まれる場合があり、これらの要素を考慮することが重要です。
- データのステーショナリティ: 時系列データがステーショナリティを持っている場合、予測がより信頼性が高まります。
- 適切なモデルの選択: 時系列データの特性に応じて適切なモデルを選択することが重要です。
まとめ
データ分析は、ビジネスにおいて重要な意思決定の支援ツールとして広く活用されています。本記事では、さまざまなデータ分析手法の概要とビジネスへの応用について解説しました。
適切な手法を選択し、正確な解析を行うことで、企業の成長や競争力の向上に大きく貢献します。ビジネスマンは、データ分析の重要性を認識し、積極的に活用することで、より効果的な意思決定を行うことができるでしょう。
XTVでは簡易なデータ分析を承っております。ぜひご依頼ください。


